Python Pytorch

Linear Regression with Pytorch

There are two ways to compute a simple linear regression using Pytorch. One is to use the optimizer update method, and one is to use vanilla update without optimize update. The two approaches are illustrated below.

# Using the optimizer update approach

import torch

learning_rate = 0.001

X = torch.tensor([1.,2.,3,4,5])
y = torch.tensor([0,-1.1,-1.8,-3.1,-4.5])

W = torch.rand(1,requires_grad=True)
b = torch.rand(1,requires_grad=True)

optimizer = torch.optim.SGD([W,b],lr=learning_rate)

for i in range(1000):
    # Model = Prediction
    yhat = X*W+b

    # Loss Function
    loss = (yhat-y).pow(2).sum()

    #Compute gradient
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    print('i=',i,'W=',W.detach().numpy(),'b=',b.detach().numpy(),'loss=',loss.detach().numpy())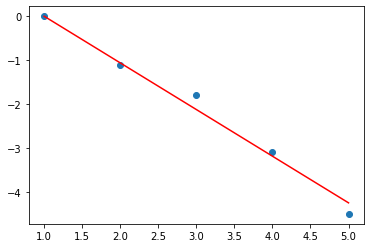

# Using Vanilla update method 

import torch
from torch.autograd import Variable

learning_rate = 0.001

X = torch.tensor([1.,2.,3,4,5])
y = torch.tensor([0,-1.1,-1.8,-3.1,-4.5])

W = Variable(torch.randn(1), requires_grad=True)
b = Variable(torch.randn(1), requires_grad=True)
optimizer = torch.optim.SGD([W,b],lr=learning_rate)

for i in range(1000):
    yhat = X*W+b

    loss = (yhat - y).pow(2).sum()
    loss.backward()

    W.data -= learning_rate * W.grad.data
    b.data -= learning_rate * b.grad.data

    W.grad.data.zero_()
    b.grad.data.zero_()
    
    print('i=',i,'W=',W.detach().numpy(),'b=',b.detach().numpy(),'loss=',loss.detach().numpy())
    
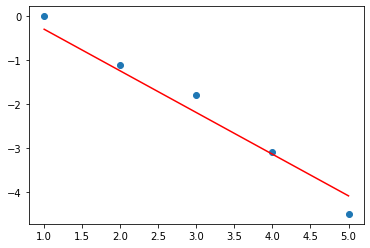
# Without the Variable

import torch
learning_rate = 0.001

X = torch.tensor([1.,2.,3,4,5])
y = torch.tensor([0,-1.1,-1.8,-3.1,-4.5])

W = torch.randn(1, requires_grad=True)
b = torch.randn(1, requires_grad=True)

for i in range(1000):
    yhat = X*W+b

    loss = (yhat - y).pow(2).sum()
    loss.backward()

    W.data -= learning_rate * W.grad.data
    b.data -= learning_rate * b.grad.data

    W.grad.data.zero_()
    b.grad.data.zero_()
    
    print('i=',i,'W=',W.detach().numpy(),'b=',b.detach().numpy(),'loss=',loss.detach().numpy())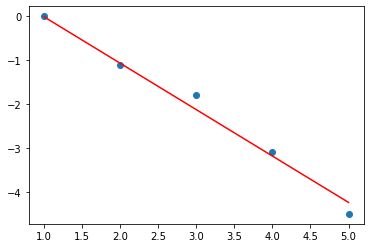
In PyTorch, we need to set the gradients to zero before starting to do backpropagation because PyTorch accumulates the gradients on subsequent backward passes. This is convenient while training RNNs.Because of this, when you start your training loop, ideally you should zero out the gradients so that you do the parameter update correctly. Else the gradient would point in some other direction than the intended direction towards the minimum

References:

Relevant Courses

July 4, 2021
,